Класс разбит на 5 групп по 5-6 человек - отделы, возглавляемые "главными инженерами". Все "сотрудники" отдела ( члены команд ) подчиняются непосредственно "главному инженеру" своего отдела, а также "руководителю конструкторского бюро" - учителю математики.

1. Ярмарка.

1. На промежутке (0;2) y'(x)>0, на промежутке (2;3) y'(x)<0. Является ли точка х = 2 точкой минимума?

2. Функция y(x) непрерывна в точке х = 3, причем y'(x)<0 на (2;3) и y'(x)>0 на промежутке (3;4). Является ли точка х = 3 точкой максимума?

3. вляется ли точка х = 2 критической для функции y(x), если Д(y) = [-3;2]?

4. Для функции y = 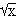производная равна 1/(2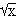). В точке х = 0 производная не существует, значит х = 0 - критическая точка. Верно ли?

5. На отрезке [a;b] функция имеет максимумы, равные 2 и 5, причем y(a) = -3 и y(b) = 6. Верно ли, что наибольшее значение функции равно 5, а наименьшее значение равно -3?

2. Лото.

Эта игра проводится в каждой группе.

1. y(x) = 4x² - 1, y'(2) - ?
2. y(x) = 9 - 4x², y'(-2) - ?
3. y(x) = 16x² - 9x, y'(1/2) - ?
4. y(x) = 4 - 25x², y'(x) - ?, x = 1/2.
5. y(x) = 10x - 18x², y'(1/2) - ?
6. y(x) = (2 + x²)/x, y'(-1) - ?
7. y(x) = (1 - 2x²)/x, y'(-1) - ?
8. y(x) = (4 - 3x)/x, y'(-1) - ?
9. y(x) = (2 - 5x)/x, y'(-1) - ?
10. y(x) = (3 - 4x)/x, y'() - ?

3. Дело.

Основная часть деловой игры, где каждый отдел занят решением практической задачи. Происходит процесс применения знаний на практике. Ведется беседа об оптимальных вариантах решения задач. Знакомство с различными профессиями. Например, можно рассказать об использовании отводного желоба в очистных сооружениях. Он строится из железобетона и внутри облицован плиткой.

При проектировании строительства этого сооружения необходимо учитывать принцип экономичности: выбрать минимальные размеры при максимальной пропускной способности.

Задачи для отделов:

1. "Облицовка".

   Заготовленной плиткой нужно облицевать 6000 кв. м боковых стенок и дна желоба прямоугольного поперечного сечения длиной 1000 м. Каковы должны быть размеры сечения, чтобы пропускная способность желоба была наибольшей?

2. "Максимальный слив".

   Необходимо построить открытый желоб прямоугольного сечения для стока воды. Длина периметра поперечного сечения желоба должна равняться 6 м. Какой высоты должны быть стенки желоба, чтобы получился максимальный слив?

3. "Два поезда".

   Два железнодорожных пути пересекаются под прямым углом. К месту пересечения одновременно мчаться по этим путям два поезда: один со станции, находящейся в 40 км от пересечения, другой со станции, находящейся в 50 км от того же места пересечения. Первый делает в минуту 800 м, второй 600 м. Через сколько минут, считая с момента отправления, поезда были в наименьшем взаимном расстоянии? Как велико это расстояние?

4. "Автомобиль".

   Для стоянки машин выделили площадку прямоугольной формы, примыкающую одной стороной к стене здения. Площадку обнесли с трех сторон металлической сеткой длиной 200 м, и площадь ее при этом оказалась наибольшей. Каковы размеры площадки?

5. Занимательная задача, связанная с рассказом Л.Н. Толстого "Много ли человеку земли надо".

   Задача: Из всех четырехугольников с периметром 40 м указать четырехугольник наибольшей площади.

   Учащимся предлагается начертить известные четырехугольники: ромб, прямоугольник, квадрат, трапецию с периметром 40 м наибольшей площади. Можно предложить составить таблицу для вычисления площадей прямоугольников с различными длинами сторон.

   Вывод: из всех прямоугольников данного периметра наибольшую площадь имеет квадрат.

3. Наши ошибки.

В конце игры предлагаются для обсуждения вопросы, которые содержат часто встречающиеся ошибки.

1. Определяя точки минимума функции, учащийся нашел, при каких значениях аргумента значения функции равны 0. Затем из этих значений он выбрал те, проходя через которые функция меняет знак с "-" на "+". Эти точки он назвал точками минимума. Прав ли он?

2. Определяя точки минимума функции, учащийся нашел те значения аргумента, при которых производная обращается в 0. Эти точки он назвал точками минимума. Прав ли он?

3. График производной. Определяя точки минимума, ученик указал точку х = 2. Прав ли он?

   

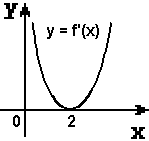
   График производной. Определяя точки минимума, ученик указал точки х = -4, х =1, х = 3. Прав ли он?

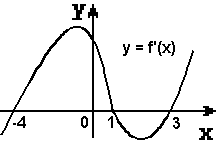   о

   График производной. Определяя точки максимума, ученик указал точку х = -2. Прав ли он?

   

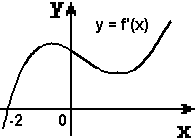
Работа каждой группы ( отдела ) оценивается баллами по результатам работы на всех этапах игры, а именно:

а) ответы по теме "Применения производной,

б) понимание условия задачи,

в) составление математической модели и выполнение преобразований,

г) исследование функции на наибольшее и наименьшее значения и получение результата,

д) применение полученных результатов к конкретным условиям и объяснение экономической выгоды.