| Решения задач 2 этапа |
|
1. Докажите, что уравнение a2xyz+adxy+acxz+abyz+(c+d)x+(b+d)y+(b+c)z+e=0, где a, b, c, d, e - целые, имеет конечное количество решений в целых числах, если ae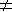 bcd. bcd.
Решение:
Раскроем скобки в произведении:
(ax + b)(ay + c)(az + d) = a3xyz + a2byz + a2cxz + a2dxy + abcz + abdy + acdx + bcd = a(a2xyz + abyz + acxz + adzy + cdx + bcz + bdy) + bcd.
Очевидно, если целые x, y, z удовлетворяют исходному уравнению, то данное произведение равно bcd-ae. Так как это число отлично от 0 (по условию), то у него конечное число делителей. Следовательно, каждое из чисел (ax + b), (ay + c) и (az + d) принимает конечное число значений. А так как a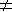 0, то и каждое из чисел x, y, z принимает конечное число значений. Поэтому и троек (x, y, z), удовлетворяющих исходному уравнению, лишь конечное число. 0, то и каждое из чисел x, y, z принимает конечное число значений. Поэтому и троек (x, y, z), удовлетворяющих исходному уравнению, лишь конечное число.
|
|
2. Неотрицательные действительные числа x, y, z удовлетворяют соотношению: x2+y2+z2=1. Докажите неравенство 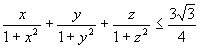
Решение:
Умножим обе части исходного неравенства на 2, получим равносильное неравенство:
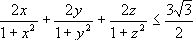 (*) (*)
Очевидно (по условию), что 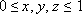 . .
Сделаем замену:
x = tg α, y = tg β, z = tg γ, где α, β, γ 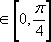 .
Очевидно, функция ƒ(t) = tg2t является выпуклой вниз на .
Очевидно, функция ƒ(t) = tg2t является выпуклой вниз на  . Запишем неравенство Йенсена для этой функции и α, β, γ: . Запишем неравенство Йенсена для этой функции и α, β, γ:
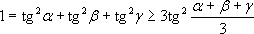 ,
откуда ,
откуда 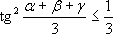 , поэтому , поэтому 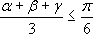 .
После подстановки x = tg α, y = tg β, z = tg γ в (*) получаем равносильное неравенство: .
После подстановки x = tg α, y = tg β, z = tg γ в (*) получаем равносильное неравенство:
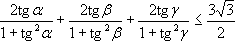 ,
что после выражения синуса через тангенс половинного аргумента можно записать следующим образом: ,
что после выражения синуса через тангенс половинного аргумента можно записать следующим образом:
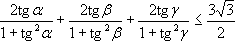 .
Докажем это неравенство. .
Докажем это неравенство.
Очевидно, функция g(t) = sin 2t является выпуклой вверх на 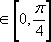 . Запишем неравенство Йенсена для функции g(t) и α, β, γ: . Запишем неравенство Йенсена для функции g(t) и α, β, γ:
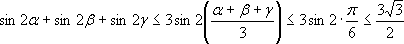 . .
Неравенство доказано.
|
|
3. Занумеруйте все клетки бесконечной клетчатой доски натуральными числами (все числа должны быть использованы по одному разу), чтобы в каждой горизонтали и в каждой вертикали все числа были попарно взаимно просты.
Решение:
Поставим 1 в любую клетку, после чего последовательно будем расставлять последовательно остальные натуральные числа. Перед тем, как поставить очередное число, смотрим, какие у него простые множители и рассматриваем все клетки, для которых в их строках и столбцах этих простых множителей нет. Такие клетки всегда найдутся, так как занумеровано конечное число клеток. Из всех таких клеток выбираем ту, которая ближе всего к 1. Так последовательно будут расставлены все натуральные числа. Докажем, что при этом заполнятся все клетки. Пусть на некоторой стадии расстановки какая-то пустая клетка ближе всего к 1, с ней в строке и столбце конечное число занумерованных клеток, следовательно, и "недопустимых" простых делителей. Тогда в этой клетке когда-нибудь обязательно в некоторый момент окажется число (по крайней мере, не позже, чем будем размещать следующее простое число).
Примечание: в качестве расстояния между клетками можно рассматривать расстояние между их центрами; если таких клеток оказалось несколько, то можно в качестве ближайшей рассматривать клетку с наименьшей абсциссой, а если и таких клеток несколько, то клетку еще и с наименьшей ординатой в системе координат с центром в клетке с номером 1 и осями, идущими вдоль линий сетки.
|
|
4. На королевском приеме собрались n рыцарей и n дам. Известно, что каждый рыцарь знаком более чем с 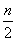 дамами и наоборот. Докажите, что всех 2n человек можно рассадить за круглым столом так, чтобы рядом с каждой дамой сидели два знакомых ей рыцаря. дамами и наоборот. Докажите, что всех 2n человек можно рассадить за круглым столом так, чтобы рядом с каждой дамой сидели два знакомых ей рыцаря.
Решение:
Рассмотрим двудольный граф, в котором вершинами одной доли являются дамы, а вершинами другой доли - рыцари. Соединяем две вершины ребром, если дама и рыцарь знакомы. По условию степень каждой вершины больше n/2. Необходимо доказать, что существует цикл, проходящий по всем вершинам графа ровно один раз (гамильтонов цикл). Предположим, что такого цикла нет, тогда будем добавлять по одному ребру, соединяющему разные вершины из разных долей, еще несоединенные ребром, до тех пор, пока в графе не появится гамильтонов цикл. Предположим, добавили ребро AB (A - рыцарь, B - дама), после чего в графе появился гамильтонов цикл, который раньше не существовал. Тогда ребро AB входит в этот гамильтонов цикл.
Пусть этот цикл A-B-A1-B1-A2-B2-...-An-1-Bn-1-A (по вершинам). Удалим из этого цикла ребро AB (вернемся на шаг назад). Заметим, что если A соединен ребром с Bi, то B не соединен ребром с Ai+1, так как иначе уже в этом графе будет гамильтонов цикл
A-Bi-Ai-Bi-1-...-B-Ai+1-Bi+1-Ai+2-...-Bn-1-A, что противоречит тому, что мы добавили ребро AB. Поэтому из пары Bi, Ai+1 не более одного ребра выходит к A или B. Отсюда следует, что все дамы и рыцари разбиваются на такие пары, кроме A1 и Bn-1. Всего таких пар n-2, поэтому суммарная степень вершин A и B не больше (n-2)+2 (добавляем 2 за счет ребер ABn-1 и BA1). Тогда степень какой-либо из этих двух вершин не превосходит n/2. Но мы не удаляли ребер исходного графа (удалили только добавленное ребро AB, что равносильно тому, что его не добавляли вовсе), поэтому степень какой-то из вершин в исходном графе не превосходит n/2, что противоречит условию. Полученное противоречие доказывает утверждение задачи.
|
|
5. Вневписанные окружности ΩA, ΩB, ΩC касаются сторон (или их продолжений) треугольника ABC в точках XYZ, где X, Y и Z - одна из букв A, B, C, т.е. окружность ΩX касается стороны YZ треугольника ABC в точке XYZ.
Прямые CACCBC и BBABBC пересекаются в точке P. Докажите, что PABC параллельна биссектрисе угла A треугольника ABC
Решение:
Обозначим длины сторон BC, AC и AB треугольника через a, b, c соответственно, полупериметр треугольника ABC равен p, 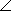 BAC = x, BAC = x, 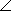 ABC = y, ABC = y, 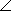 BCA = z. BCA = z.
По свойству вневписанных окружностей:
BCBC = p-a, BABC = p-c, CABC = p-b, CBBC = p-a.
Из этого следует, что ABCCBC = p-a+p-c = b, BBCABC = p-a+p-b = c.
Также заметим, что 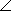 ABCBBCP = ABCBBCP = 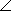 ABCBBCBBA = 90o-y/2. ABCBBCBBA = 90o-y/2.
Аналогично ABCCBCP = 90o-z/2.
Проведем биссектрису BL, точка K - точка пересечения прямой BL и BBABBC, I - точка пересечения этой биссектрисы с биссектрисой угла A. Тогда I лежит между B и K, 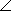 IKP = 90o, IKP = 90o, 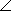 AIK = (x+y)/2. Поэтому угол между биссектрисой угла A и BBCBBA равен 90o - (x+y)/2 = z/2. AIK = (x+y)/2. Поэтому угол между биссектрисой угла A и BBCBBA равен 90o - (x+y)/2 = z/2.
Проведем через точку P прямую, параллельную биссектрисе угла A. Пусть она пересечет сторону BBCCBC в точке X. Тогда 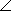 BBCPX = z/2, BBCPX = z/2, 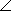 CBCPX = y/2. По теореме синусов для треугольников BBCPX и CBCPX получаем: CBCPX = y/2. По теореме синусов для треугольников BBCPX и CBCPX получаем:
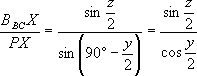 , ,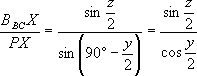 . .
Отсюда следует:
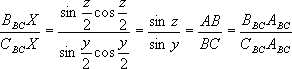 . .
Но так как обе точки лежат на отрезке BBCCBC, то они совпадают (точка ABC лежит на отрезке BBCCBC, а точка X лежит по построению, так как 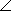 BBCPX меньше BBCPX меньше 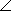 BBCPC и откладывается в ту же сторону). Поэтому PABC параллельна биссектрисе угла A. BBCPC и откладывается в ту же сторону). Поэтому PABC параллельна биссектрисе угла A.
|
 |
 |
|
 |
|



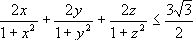 (*)
(*)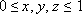 .
.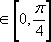 .
Очевидно, функция ƒ(t) = tg2t является выпуклой вниз на
.
Очевидно, функция ƒ(t) = tg2t является выпуклой вниз на  . Запишем неравенство Йенсена для этой функции и α, β, γ:
. Запишем неравенство Йенсена для этой функции и α, β, γ:
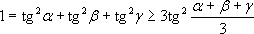 ,
,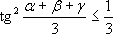 , поэтому
, поэтому 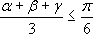 .
После подстановки x = tg α, y = tg β, z = tg γ в (*) получаем равносильное неравенство:
.
После подстановки x = tg α, y = tg β, z = tg γ в (*) получаем равносильное неравенство: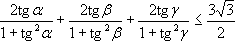 ,
,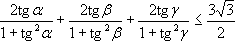 .
.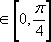 . Запишем неравенство Йенсена для функции g(t) и α, β, γ:
. Запишем неравенство Йенсена для функции g(t) и α, β, γ: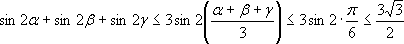 .
.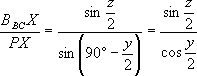 ,
,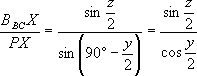 .
.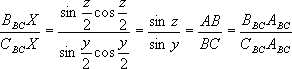 .
.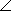 BBCPX меньше
BBCPX меньше 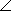 BBCPC и откладывается в ту же сторону). Поэтому PABC параллельна биссектрисе угла A.
BBCPC и откладывается в ту же сторону). Поэтому PABC параллельна биссектрисе угла A.
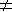 bcd.
bcd.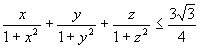
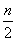 дамами и наоборот. Докажите, что всех 2n человек можно рассадить за круглым столом так, чтобы рядом с каждой дамой сидели два знакомых ей рыцаря.
дамами и наоборот. Докажите, что всех 2n человек можно рассадить за круглым столом так, чтобы рядом с каждой дамой сидели два знакомых ей рыцаря.